いろいろな例題 順列に関する基本的なタイプの問題を $3$ 種類紹介します. 並べる順番を工夫する 例 $6$ 個の数字 $0,1,2,3,4,5$ から異なる $4$ 個を並べて,$5$ の倍数であるような $4$ 桁の整数は何個つくれるか. $4$ 桁の数字をつくる問題です.単純に選んだ数を左から並べるとする左の数から始まり、1つずつ数を減らしながら右の数だけ掛け算をしていきます。 上の式であれば、「6ピー3」と読みます。 文字で書くとなんだか変な感じだけどね 6と3の間に何が起きたんだ!みたいなw 順列pの基本計算 数 A 場合の数と確率 順列 P とは? 公式や計算方法、問題の解き方(重複ありなど) 21年2月19日 この記事では、「順列」の公式や問題の解き方をできるだけわかりやすく解説していきます。 重複順列の問題なども紹介していきますので、この記事を

3講 順列 1章 場合の数と確率 問題集 高校数学a
数a 順列 組み合わせ 問題
数a 順列 組み合わせ 問題-前回 https//wwwyoutubecom/watch?v=gkeQK_kfa5w 次回 https//wwwyoutubecom/watch?v=4LJtn7VG67Mサブチャンネル とある男がゲームを小学6年生の算数 場合の数・順列 練習問題プリント ツイート 組み合わせ方、並べ方を、落ちや重なりがないように順序よく整理して、調べる方法を練習できる問題プリントです。 場合の数・順列(1) 答え 場合の数・順列(2) 答え 場合の数




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ
数 学 A 場合の数 例題(9) 練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題+解答整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線 この講から、本格的な場合の数の問題に入っていきます。 まずは順列。 教え方がマズいと、「Pなの?Cなの?」といういけてない疑問が生じますが、Pはただの省略の記号であって、考える上では全く使いません。 安直に、一発で答えが出ると思わずに、迷ったら、何パターンでも場合練習問題 順列と組合せの問題を混ぜました。 順列と組合せの違い 順列 :「選んで並べる」「ABとBA を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「ABとBAは区別せず同じもの」 に注意しながら,考えてみてください。 例題3 (1) 5
F 48通り 「QとRの2人を続けて並べる」という条件があるので、 まずQとRの2人を1つのグループにまとめ、 「1つのグループ」と「他の3人」の計4つの並び順 が何通りあるかを考える。 式) 4 P 4 = 4×3×2×1 = 24(通り) QとRの並び順については、「Q→R」と「R 組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列 $\rightarrow$ 順序を考慮 (区別)する.場合の数(順列)入門 5人を横一列に並べる 何通りあるかを求める問題を「場合の数」と言います。 中学,高校でも習いますが、受験算数では超頻出で簡単な問題から超難問まで出題されます。
N C r の関係があるが順列Pの公式と使い方を徹底解説! 5分で分かる順列のコツ! 「順列の公式ってなんだっけ? 」 今回はこんな悩みを解決します。 順列の問題がすごく苦手なんですよ 数学Aでは順列や組み合わせをつかってそれぞれの事象の場合の数を求めますについてパターン別に解説していきます。 取り上げる問題はこちら! 問題①(0を含まないパターン) 6個の整数 , , , , , から異なる3個の数字を選んで3桁の整数をつくるとき,次のような数の個数を求めよ。 (1)すべての整数 (2)偶数 (3)4の



1




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学
攪乱順列のことを 完全順列 とも言います。 攪乱順列の方が漢字は難しいですが,意味は分かりやすいと思います。 n n n 個の場合の攪乱順列の数 a n a_n a n は モンモール数 とも呼ばれます。;順序を区別すれば,項の数は「重複順列」 2 3 =8 通りになる =a 3 3a 2 b3ab 2 b 3 文字の部分が同じものを同類項として整理すれば,文字の組合わせは a 3 , a 2 b , ab 2 ,b 3 で 2 H 3 =4 種類になる ※ これらのうち,順列と組合せには, n P r =r!例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 p 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note
順列の場合の数の求め方は覚えているかな? 「異なる5人を1列に並べる」 ときは、 5 p 5 =5! (通り) だね。 このうち 「両端が女子になる」 のはどう求める?「条件」を先に考える のがコツだったよね。 つまり、両端の女子を先に並べて、 (先頭の女子3通り) × (いちばん後ろの女子2通り) 。 高校数学A 場合の数 組分けは単純な問題は教科書レベルの基本問題であるが、実際には「モノが区別できるか否か」「組が区別できるか否か」「組の要素の個数が決まっているか否か」「要素の個数が0個の組があってもよいか」で求め方が変わる裏返して一致するものは 同じものと考えられるので数珠順列 の 考え方を用いて計算していきます。 円順列の場合の数の中に表と裏の 2 パターンがあるので 円順列の半分になります。 したがって,異なる 個のものを数珠順列にすると,場合の数は, と




基本問題 場合の数3 順列 0を含む順列と倍数 No Youtube




高1数学の順列です 2番の問題がわからないです 教えてください Clear
順列の特訓プリントです (`・ω・´) 図を描くのが解くためのカギです (*´ω`*) 数学A 順列 人を並べる特訓① 数学A 順列 桁数問題特訓① 数学A 順列 辞書式配列・小さい順特訓① 数学A 順列 円順列 (人を並べる)特訓① 数学A 順列 円順列 (図形の色塗り)特訓①場合の数の問題は大まかに分けると 順列 と 組み合わせ があり,これらは掛け算と割り算を駆使することで求めることができます. では実際に解いてみましょう! 1a,b,cの3人を1列に並べる方法は何通りあるか. *1 解答1 書き出す解き方よって、求める場合の数は、 4+4+6+12+12=38(通り) (問題補充2) 順列・組合せの問題として、興味ある解法に出会ったので紹介したい。 14. 凸 n 角形の頂点を頂点とし、対角線を辺とする三角形は、全部で何個あるか?




数学a 怜悧玲瓏 高校数学を天空から俯瞰する



数学i Aチェック リピート 第7章 2順列 組合せ 1 重複順列 順列 Pukiwiki
場合の数 順列の計算 2 2 白玉と黒玉と赤玉がたくさんあります。 この中から2個の玉を選んで1 列に並べます。 ⑴ 1番目のご石の選び方は(ア )通り。 ⑵ 2番目のご石の選び方は(イ )通り。 ⑶ ⑴、⑵より、2個のご石の並べ方は全部で、 集合の要素の個数 場合の数 順列 円順列・重複順列 組合せ 同じものを含む順列、重複組合せ 確率 確率の基本性質 独立な試行 反復試行 図形の性質 三角形の辺の比 三角形の五心 チェバの定理、メネラウスの定理 円に内接する四角形 円と直線 方べきの定理 書き方は各自の自由だが,\ {「入れた数字」と「何通りか」をきちんと区別しよう} $一の位は1,\ 3,\ 5の3通り}である$ { }$千の位は,\ 0と一の位の数を除く4通り}がある$ { }$残りの位は,\ 4個から異なる2個を選んで並べる順列}である$ {一の位が1,\ 3,\ 5,\ 最高位が




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学
SPI 場合の数 問題31(順列)Study Pro(SPI) TOP SPI言語 SPI非言語 SPI英語 CAB 構造的把握力 TOP SPI非言語 場合の数 SPI 場合の数 順列・組み合わせの基礎 この単元の基礎は分量が多いです。 頑張って学習しましょう! ! 1 PとCの使い分けの解説です。 <問題> 1~3のカードが1枚ずつある ① 2けたの整数は何通りできるか ② 2枚選ぶのは何通りあるかつまり、順列の問題とは、 「 n個の要素を、r個の異なる席に当てはめる場合の数 」を求める問題、と言えます。 基礎的な問題では、「要素の並べ替え」でも「席に当てはめ」でも ほとんど変わらないように思えるかもしれませんが、




数の順列2 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
5 円順列 異なる6 個のビーズがある。 (1) これらのビーズを円形に並べる方法は何通りあるか。 (2) これらのビーズに糸を通して輪を作るとき,何通りの作り方があるか。 円順列 異なるn 個のものの円順列の総数は n n P n =(n-1)!場合の数と確率問題文の意味の取り方について 場合の数と確率排反事象と独立試行の違い 場合の数と確率組分けの問題の見分け方 場合の数と確率順列と組合せの見分け方;ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。




高校数学 数a 11 順列 数字の応用編 Youtube



2
問題 男子3人、女子4人が1列に並ぶとき、次のような並び方は何通りあるか。 (1) 両端が男子である (2) 女子4人が続いて並ぶ (3) 男子、女子が交互に並ぶ ある種、順列の典型問題ですので、これを通して順列の問題の考え方を学んでください。




高校数学 数a 9 順列 男女編 Youtube




3講 順列 1章 場合の数と確率 問題集 高校数学a




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ



同じものを含む順列の問題 京極一樹の数学塾




改訂版 4step数学a P103 4 円順列 重複順列



1




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




3講 順列 1章 場合の数と確率 問題集 高校数学a




高校数学a 順列の活用2 男女の並べ方 練習編 映像授業のtry It トライイット




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




順列と組合せの違いと例題 高校数学の美しい物語



3




数学a 場合の数 同じものを含む順列 Youtube




数学a 怜悧玲瓏 高校数学を天空から俯瞰する




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学
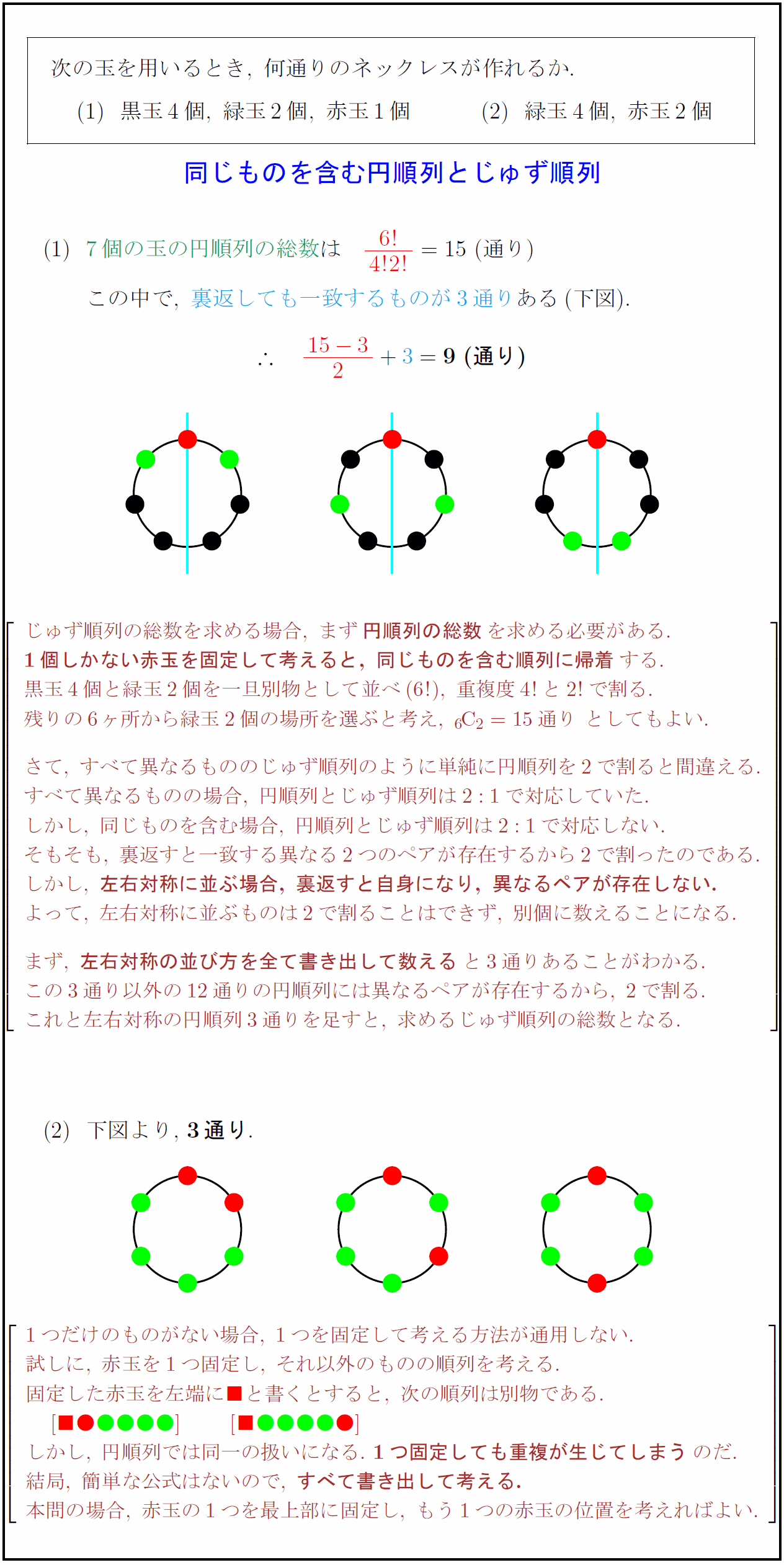



高校数学a 同じものを含む円順列とじゅず順列 受験の月




高校数学 数a 勉強動画 順列 基本編の問題 19ch




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ
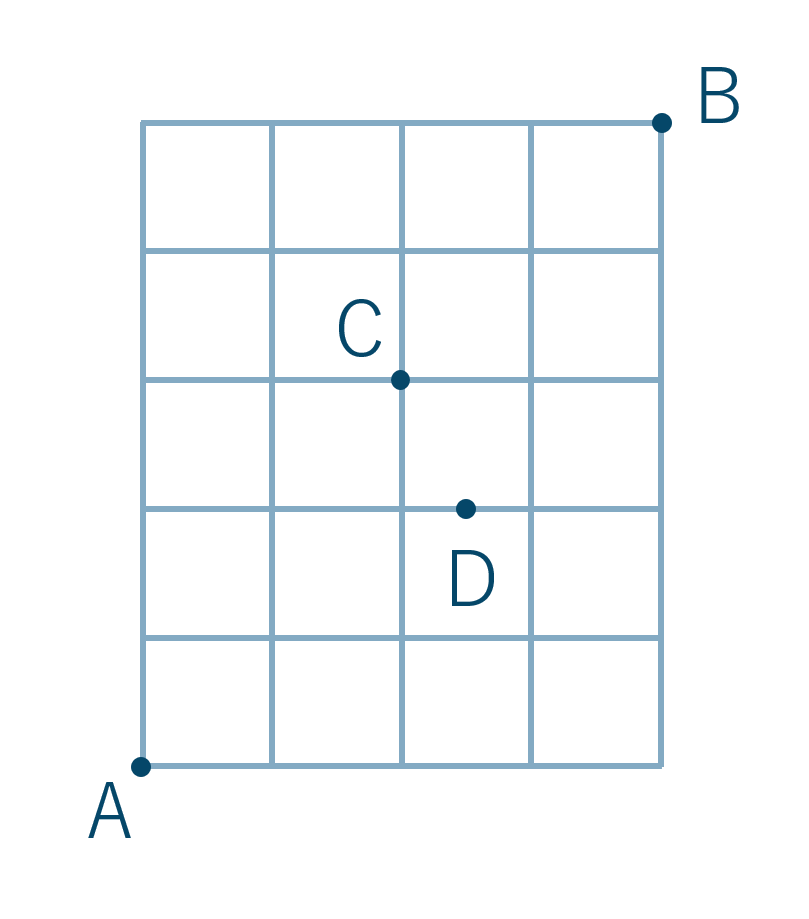



教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




高校数学a 順列の活用2 男女の並べ方 練習編 映像授業のtry It トライイット




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校数学a 同じものを含む順列 練習編 映像授業のtry It トライイット




順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ



Spi M54e217p7lcis9d Com Jyunretu Kumiawase Q1



数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



同じものを含む順列の問題 京極一樹の数学塾




高校数学 数a 勉強動画 順列 グループ分け編の問題 19ch




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



同じものを含む順列の問題 京極一樹の数学塾
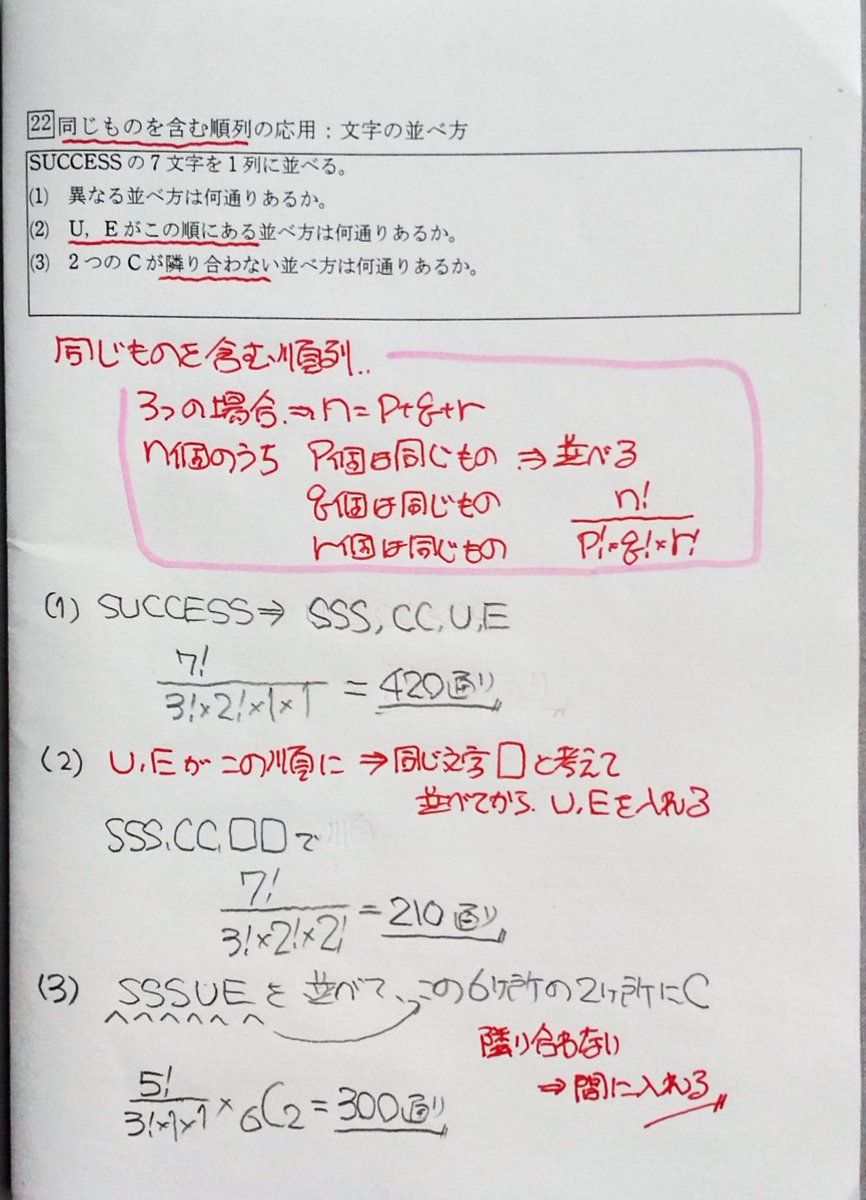



原田 浩明 Sサクシード223 組に分ける問題 同じものを含む順列 高校 数学 数a 組合せ




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月




順列と組み合わせの公式とその違い 問題付き 理系ラボ




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する




順列の問題 一定の条件で並べる 高校数学の知識庫




数学の順列の問題でよくある 仕切りを利用する問題で なぜ問題にはない仕切りを計算の中 Clear




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 重複組合せ Nhr 受験の月




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




数学の順列の問題で 文字を並べ替えて Clear



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b
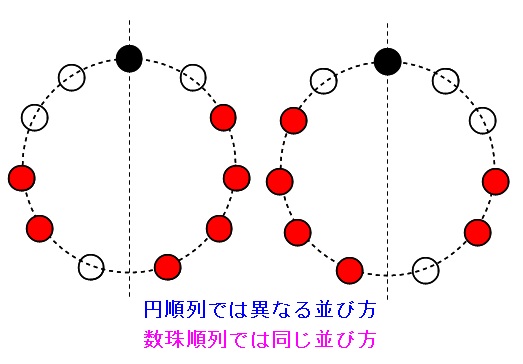



円順列と数珠順列の考え方や公式と問題の解き方




場合の数20 重複順列 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a Npr と Ncr の使い分け 映像授業のtry It トライイット




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




改訂版 4step数学a P102 4 円順列 重複順列




3講 順列 1章 場合の数と確率 問題集 高校数学a




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん



数a順列組み合わせ 2番と3番の問題について なぜ分数になる Yahoo 知恵袋




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note



確率問題全般 京極一樹の数学塾
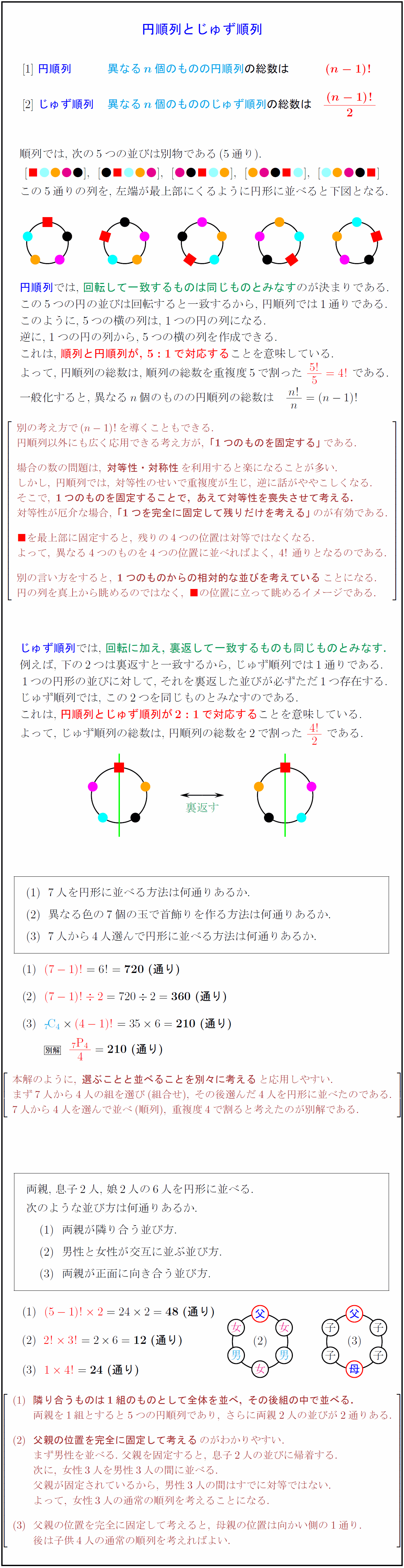



高校数学a 円順列とじゅず順列 受験の月




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学



円順列 数学入試問題




高校数学a 一定の順序を含む順列 受験の月
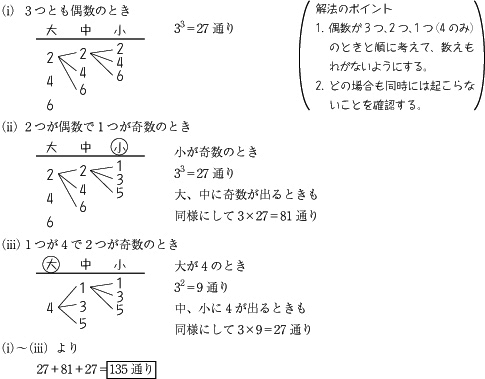



授業実践記録




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




高校数学 数a 7 順列 基本編 Youtube




高校数学 数a 勉強動画 順列 男女編の問題 19ch




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら



場合の数 学び家 Com




3講 順列 1章 場合の数と確率 問題集 高校数学a



12 鹿児島大学 入試問題から Kadaiの順列




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




数学aです 問題 Defenseの7文字から4文字を取り出す時 Eを3個含む場 高校 教えて Goo




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




高校数学a 重複順列 例題編 映像授業のtry It トライイット




高一数a 順列 この問題の解き方が分かりません 7 6 5 4 3 2 1 Clear




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




数学ia 順列に関する問題の考え方 大学入試数学の考え方と解法



数学i Aチェック リピート 第7章 2順列 組合せ 8 同じものを含む順列 Pukiwiki




順列pと組み合わせcの違いと 簡単 な見分け方



1




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




場合の数40 完全順列1 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 同じものを含む順列 N P Q R 受験の月


