円,角,垂直,平行 円と直線 平行四辺形の性質と条件 4章 平行と合同(中2学年) 5 多角形の内角と外角 拡大、縮小 対頂角、平行線の性質と条件 相似な図形、相 図形の性質の調べ方 三角形の合同条件 平行線と線分の比・平行線と錯角 〇 ・平行線の性質と平行線になるため の条件の違いを理解する。 ・対頂角の性質,平行線の性質を使 って,角の大きさを求めることが できる。 4 ・三角形の内角の和 〇 ・三角形の内角の和が180°である ことを,平行線の性質を使って説平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理(性質) 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう四角形を平行四辺形としよう」 と決めたことなので
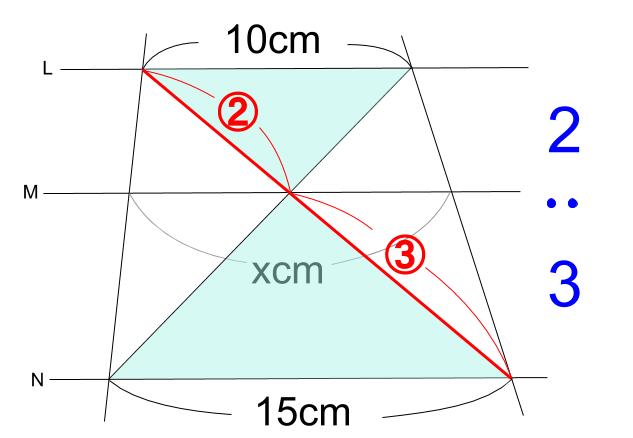
中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
平行線の性質
平行線の性質-平行線の作図 例題 点 \(a\) を通り、直線 \(l\) に平行な直線を作図しなさい。 解説 垂線を2回ひく 最終目標をは以下のようになります。 平行線の図形的性質から、作図の手順がわかります。 1.\(a\) を通▼平行線になる条件 ① 同位角が等しければ,2直線は平行である。 ② 錯角が等しければ,2直線は平行である。
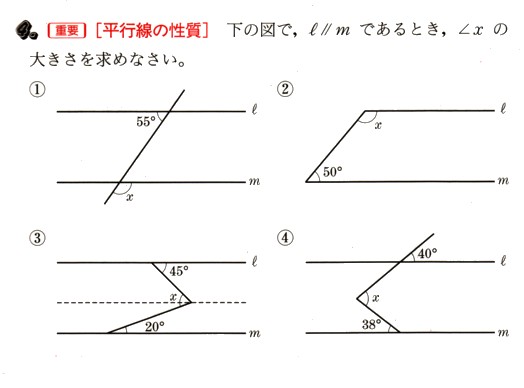



中学2年数学 図形の調べ方 平行線と角 練習問題4 あんのん塾
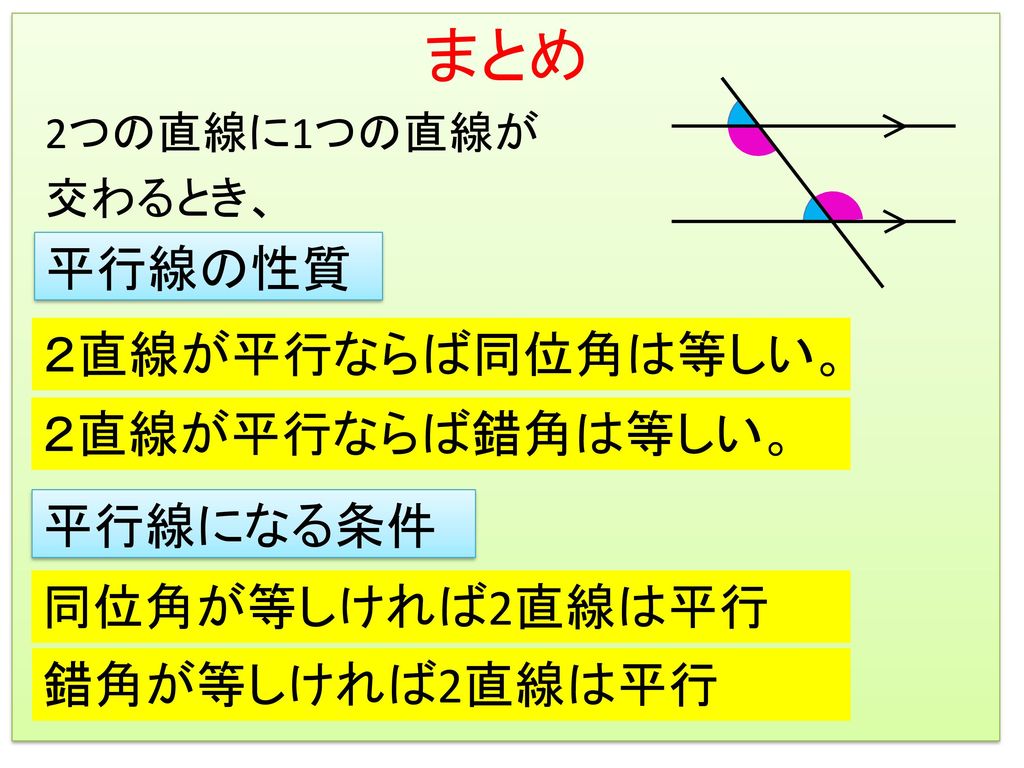
平行線の性質 内容 2つの直線に1つの直線が交わるとき、次のことが成り立つ。 ①2つの直線が平行ならば、同位角は等しい。 ②2つの直線が平行ならば、錯角は等しい。 <戻る>9 2平行線 と比 ①三角形 と比 三角形における平行線と 比の性質について理解し,そ れを利用して線分の長さを 求めたり,図形の性質を証明 したりすることができる。 ノートの罫線を3等 分する方法とその方法 で3等分できるわけを 考える。・前時に学習した平行線と角の性質を使いいろいろな角度を求めることができる。 情報教育目標リスト(11年版) A51b3000: 情報の整理・分析のためにコンピュータや情報機器を活用する〔〕
結定理,平行線と比の定理を結定理,平行線と比の定理 ををを 利用して線分の長さや新た な図形の性質を考える。 な図形の性質を考える。 8 本本本 時時時 7/877//7/8 討論・協同 解釈・説明 相似な図形の相 似比と面積比平行線の性質,三角形の 角についての性質,三角 形の合同条件などについ ての基礎的・基本的な知 識や技能を活用して,論 理的に考察し表現するな ど,数学的な見方や考え 方を身に付けている。 平行線の性質,三角形の 角についての性質,三角単元 平行と合同 1.単元の目標 (1)様々な事象を平行線の性質,三角形の角についての性質,三角形の合同条件などで捉えたり,平面図形の基本的な性質や関係を見いだしたりするなど,数学的に表現することに関心をもち,意欲的に問題解決に活用して考えたり判断したりしようとしている。
平行線の性質,平行線であるための条件を理解 ・自力解決し,グループで話し合い,全体で共有する。 し,対頂角や平行線の同位角,錯角を使って,角 ・同様にして,同位角や錯角が等しければ2直線が平行に の大きさを求めることができる。平行線と面積の性質から acd= aceとなります。 よって $${四角形abcd= abc+ acd}$$ $${= abc+ ace}$$ $${= abe}$$ となるので abeは四角形abcdと面積が等しい三角形だということがわかります。「平行と合同」 2節 「平行線と角」 本時5/7 説明のもとになることが らに関心を持ち,凹四角 形の角の関係を,既習の 性質から導くことを考え ようとしている。 角の大きさの求め方を, 補助線の引き方や根拠と なる図形の性質を明らか




zとfでイメージ化して覚える 中2 平行線の同位角 錯角 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles
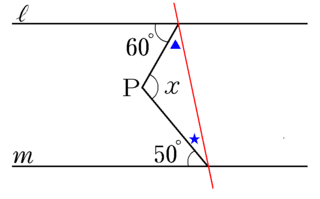



角度を求める 補助線 Takapの数学日記
平行線の性質のおさらい2(三角形) 友達にシェアしよう! すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できる わからないところを質問できる 会員登録をクリックまたは・ 平行線の性質を基に、底辺が共通な三角形について考察することができる。 段階 学習活動 数学的活動を通した指導のポイント ( は数学的活動をともなう学習活動)平面図形の性質を理解することは、算数・数学を学習する上でたいへん重要です。 その基本となるのが、平行と垂直です。 算数道場 3・図形の性質 1平行・垂直_その2




觀念 平行線判別性質 數學 均一教育平台




中学数学 平面図形と平行線の性質
3 平行線になる条件 ・平行線になる条件とその違いについて理解している。〔発言、 ワークシート〕 多 4 三角形の内角と外角 ・平行線の性質を用いて、三角形の内角の和について考えるこ 角 とができる。1.平行・垂直_その3 その3_平行線の作る角度 5年 今度は、2本の平行線にもう1本直線を加えて交わらしてみます。 すると、あちらこちらに角ができますから、その大きさの関係を覚えておこうね。 また、2本の直線の関係にはどのようなものがあるのか平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので
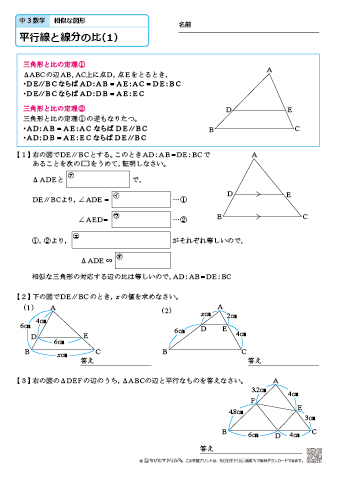



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
性質 平行線の性質, 平行線になる条 件を理解してい る。 〔小テスト〕 4 小単元2 平行線と角の性質を 多角形の角につ 「三角形の内角 「三角形の内角 年(学数学) 4学習指導案 ,2!%4 m*ñ å ± î①平行線と角 それでは、平行線と角の特徴(性質)を見ていきましょう 人は、「特徴」があると「名前」をつけたくなりますね! 口には出さなくても、心の中で「あの『茶髪君』いけてる!」などなど、 名前をつけた、=『特徴がある』 ということですね ・平行線の性質 2つの直線に1つの直線が交わる時 2つの直線が平行ならば、同位角は等しい 2つの直線が平行ならば、錯角は等しい




高校 数学a 図形4 平行線の性質2 10分 Youtube




常滑市のイチゴ狩り 朱里いちご園 朱里いちご園
味と性質を理解している。 (知) 第 2 次 ( 4 ) 2 平行線の性質や平行線に なる条件をもとに、新たな 性質を見いだす。 ・三角形の内角の和 ・三角形の1つの外角は、その となりにない2つの内角の 和である の式を比較し、話し合う活 ・角の分類、三角形平面図形 三角形の性質 三角形の辺と角の大小 例題 練習問題 三角形の3辺の大小関係 例題 練習問題 平行線と線分比 例題 練習問題 線分の内分点と外分点 例題 練習問題 線分の比と三角形の角の二等分線 例題 練習問題 面積と比 例題 練習問題 メネラ課題対頂角の性質・平行線 の性質・平行線になる条件を 使って問題が解けるかな。 課題2つの平行線に1つの 直線が交わるときにできる錯角 と同位角の大きさはどのように なるだろうか。 活動錯角と同位角の位置関係




対頂角 平行線の角 同位角 錯角 無料で使える中学学習プリント
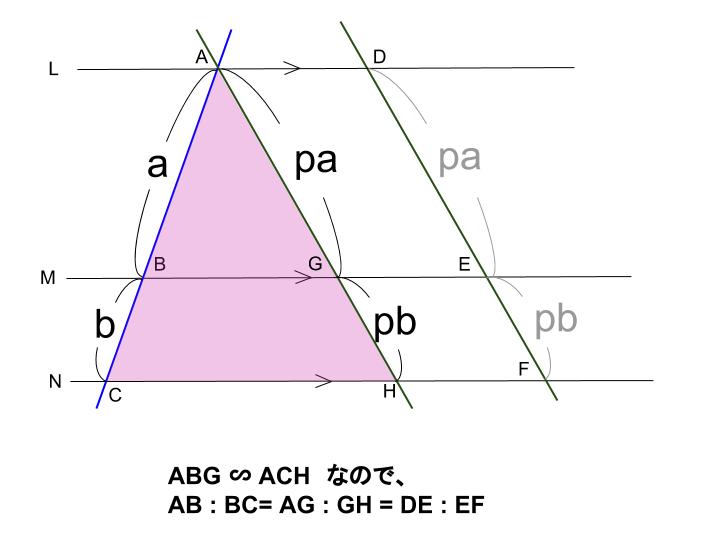



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su
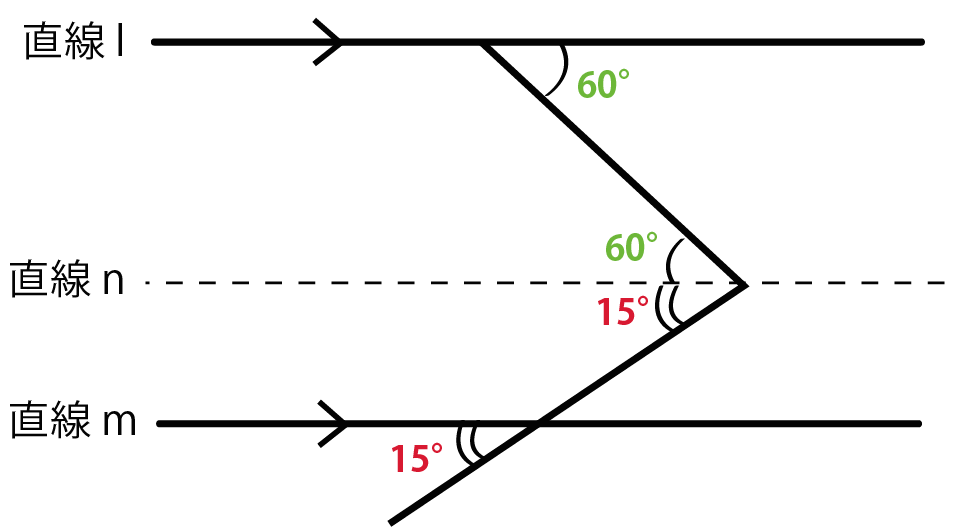
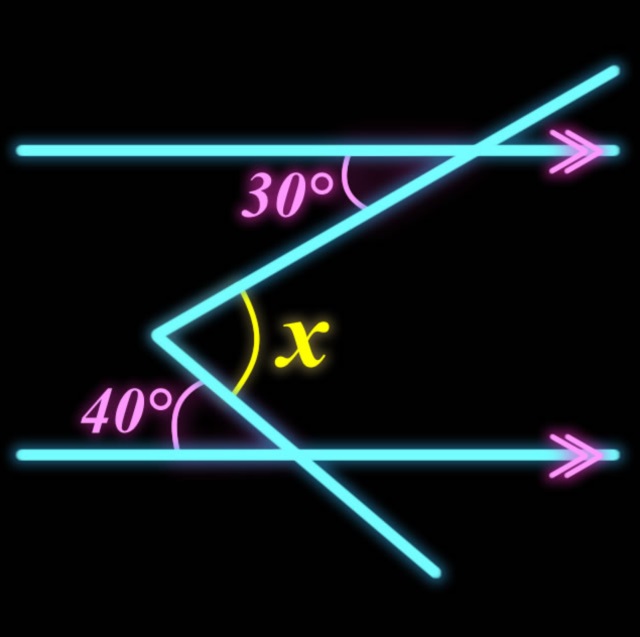
そのため、平行線の性質を使います。 しかし折れてしまっているのでこの折れている部分にも平行線の性質を使えるようにしましょう。 「折れている点に平行線を引く」ことがポイントです。 解説 (1)次の図の平行線の性質 1 同位角は等しい。 2 錯角は等しい。 (教科書p44) 三角形の内角と外角について,次の性質が成り立つ。 三角形の内角,外角の性質 1 三角形の内角の和は 180° である。平行線の錯角、同位角 平行線の定義・・・錯角の等しい2直線は平行である。 この定義から次の性質、条件が導ける。 平行線の性質 2つの直線に1つの直線が交わるとき、 2つの直線が 平行なら錯角は等しい 。 2つの直線が 平行なら同位角は等しい 。



Studydoctor平行線の性質と証明 中2数学 Studydoctor



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図)1 平行四辺形の向かい合う辺は等しい。(証明) 2 平行四辺形の向かい合う角は等しい。(証明) 3 平行四辺形の対角線は、それぞれの中点で交わる。① 平行線や角の性質に基づいて図形の性質を確かめ,説明する。 ② 平行線の性質や三角形の角についての性質を基にして,多角形の角についての性質が見いだせる ことを知る。 ③ 平面図形の合同の意味及び三角形の合同条件について理解する。平行線と線分の 比についての性質 に関心をもち、平 行線の性質を三角 形の相似条件を用 いて証明しようと している。〔観察・ ノート〕 平行線と線分の 比についての性質 を,平行線の性質 や三角形の相似条 件を用いて証明す ることができる。 〔観察



3



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく
④ 平行線の性質を用いて,平 行である2直線を見いだし たり,図形の性質を考察した りすることができる。 ⑤ 平行線の性質を用いて,三 角形の内角の和について考 察し,証明することができ る。 ⑥ 図形の性質を通して,証明 することのよさに気付いて平行線の性質・条件 直線が平行であるとき、必ず同位角、錯角のそれぞれが等しくなり 逆に、同位角、錯角がそれぞれ等しい時、2直線は平行となります。 これらは相互関係にあり、どちらかが成り立つとき、もう片方も成り立ちます!イ 平行線の性質や三角形の角についての性質を基にして,多角形の角についての性質が見いだ せることを知ること。 本単元は,図形についての数学的な推論に関する能力を伸ばし,図形について見通し




觀念 平行線的意義與性質 數學 均一教育平台




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学



毎日脳トレ 中1レベル 平行線の性質わかる Dアプリ レビュー
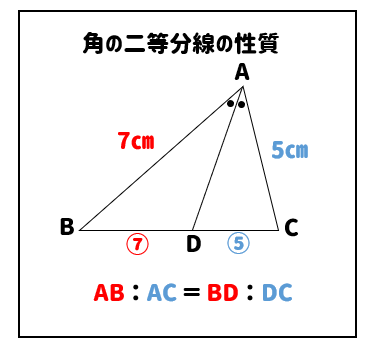



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典




中2 中2 数学 角 平行線の性質と条件 中学生 数学のノート Clear




高校数学a 平行線の性質のおさらい1 同位角 錯角 映像授業のtry It トライイット
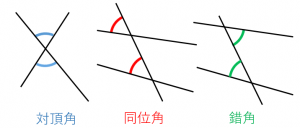



対頂角 同位角 錯角の意味を分かりやすく解説 具体例で学ぶ数学




平行四辺形の定義と性質 証明問題の解き方 数学fun
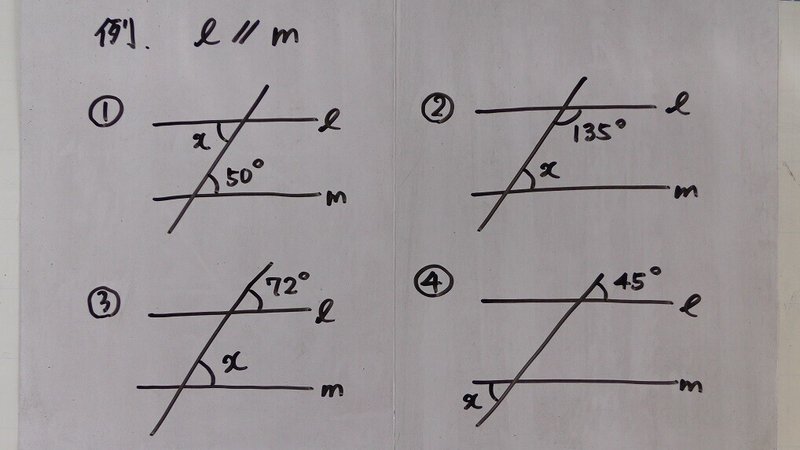



11 5 平行線の幾何 平行線の性質とその使い方 理一の数学事始め Note




高校数学a 平行線の性質のおさらい1 同位角 錯角 例題編 映像授業のtry It トライイット
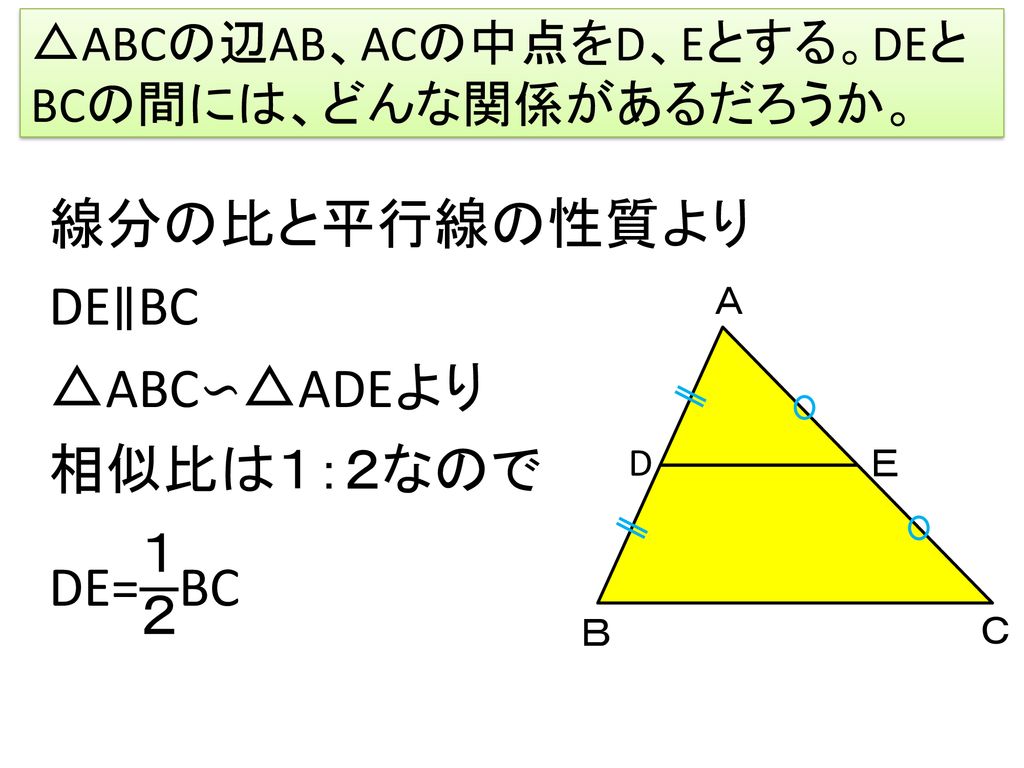



中点連結定理 本時の目標 中点連結定理を理解する Ppt Download
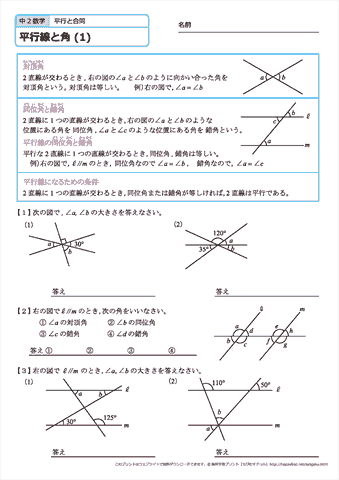



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



Ten Tokyo Shoseki Co Jp Text Chu Current Sugaku Files Thema Sugaku 09 Pdf
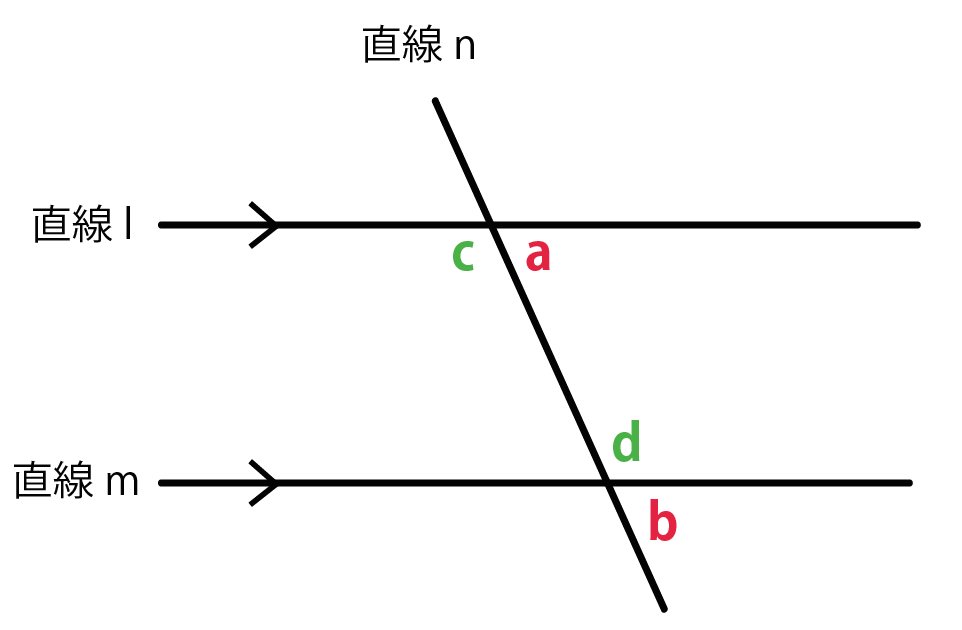



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく
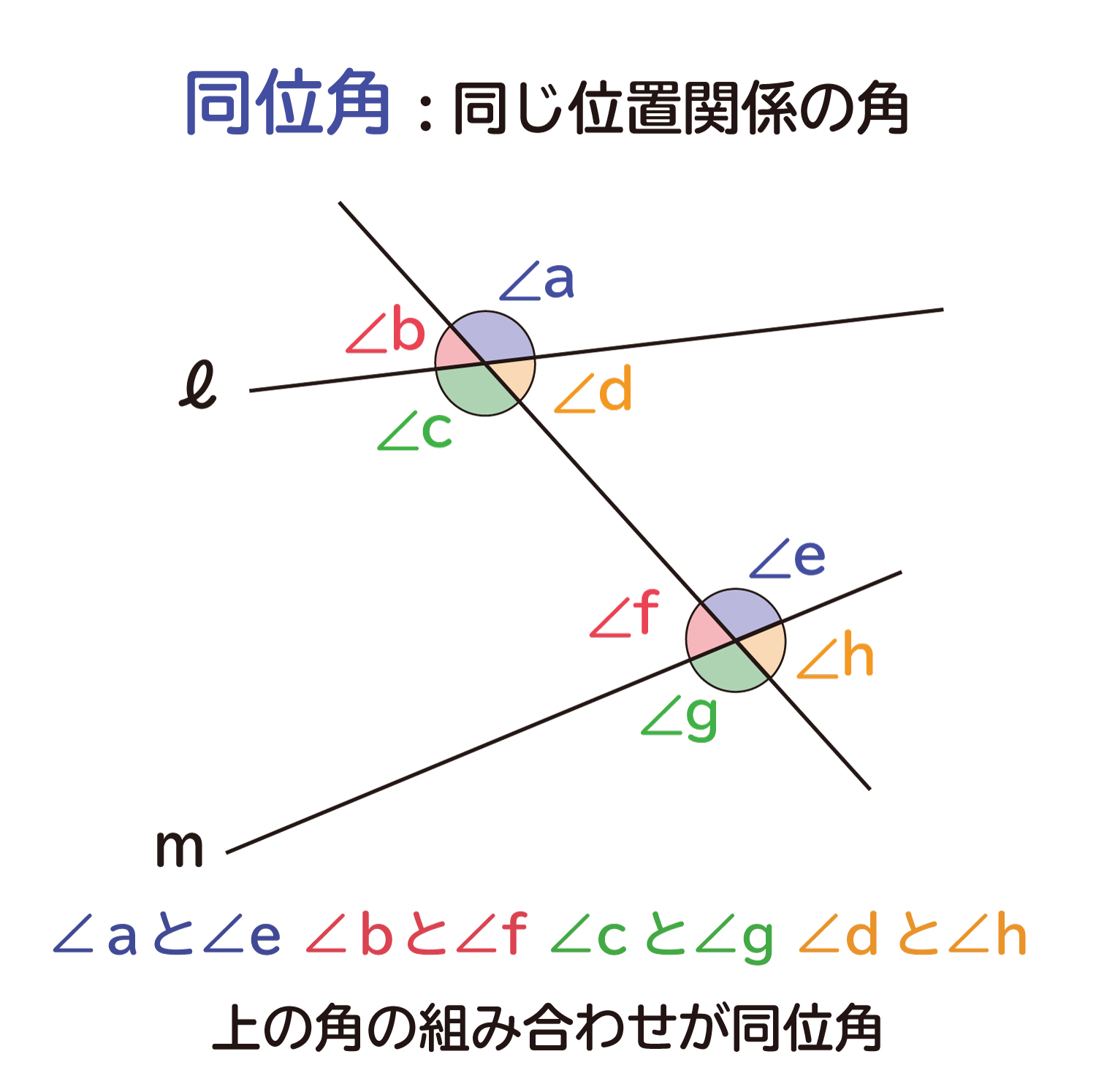



中学生の数学で出る平行線の同位角 どういかく と錯角 さっかく の性質 おかわりドリル
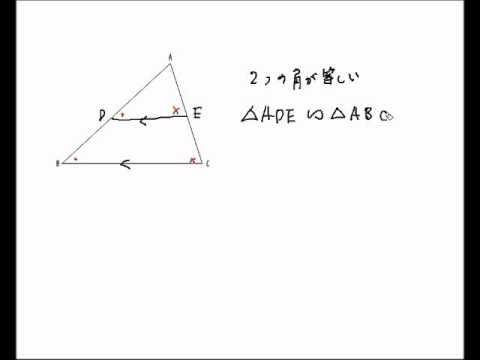



三角形と平行線の性質 Youtube
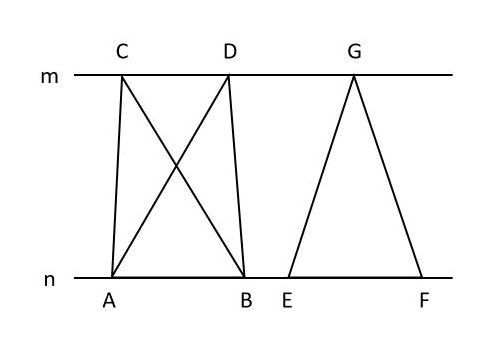



等積変形で難しい面積問題をサクッと解決 平行線と三角形の関係がおもしろい 中学受験ナビ



理由 理由一覧 仮定 共通の角 辺 対頂角の性質 平行線の性質 平行線になる条件 三角形の内角 外角の和 二等辺三角形の性質 正三角形の性質 平行四辺形の性質 平行四辺形になる条件 仮定 仮定 合同証明 理由 理由 理由 成り立つこと 成り立つこと




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




تحميل 平行線の Mp4 Mp3



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
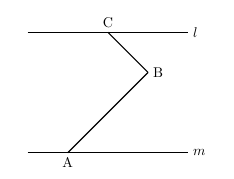



平行線と角の問題の解法 夢を叶える塾
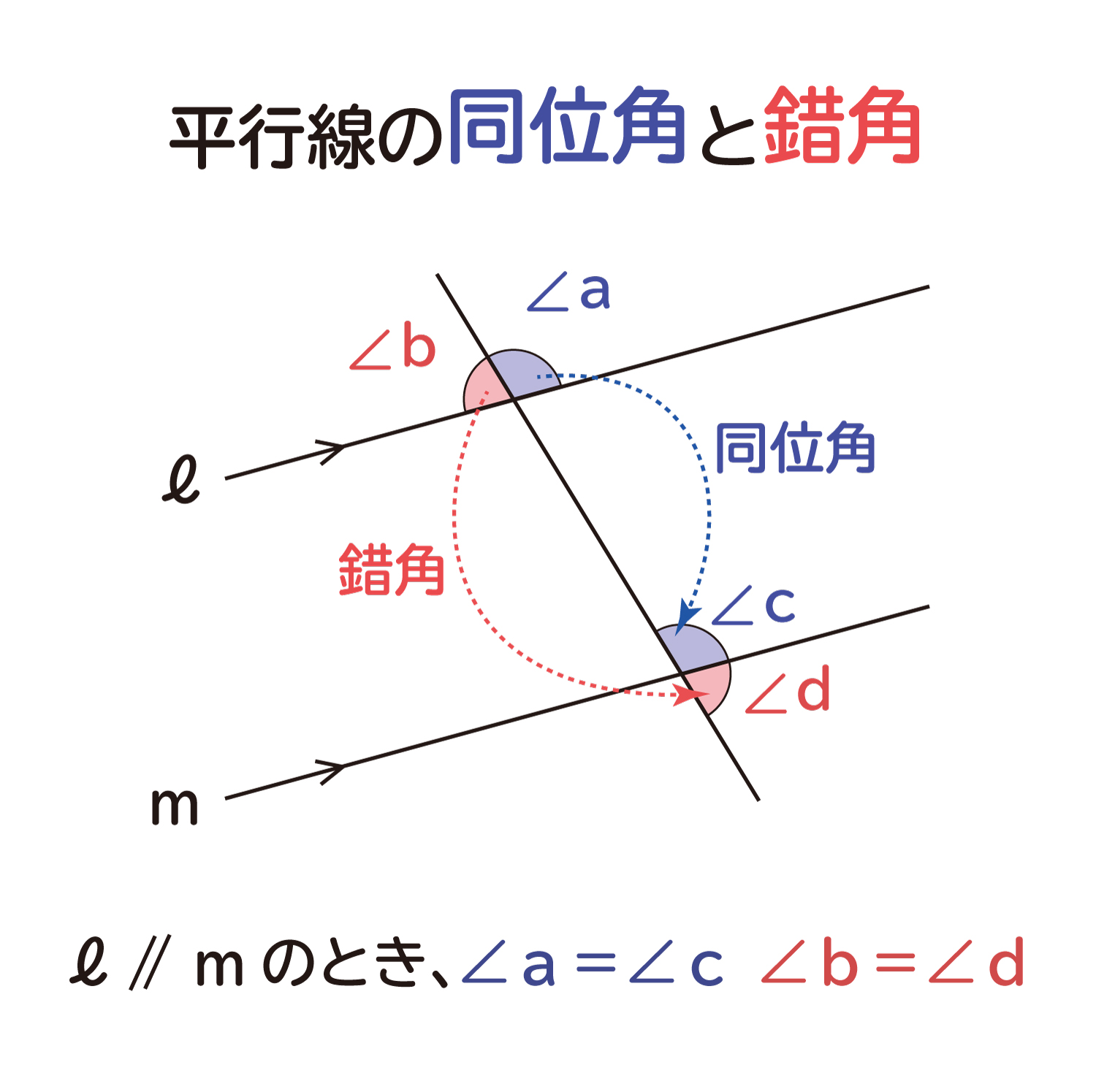



中学生の数学で出る平行線の同位角 どういかく と錯角 さっかく の性質 おかわりドリル
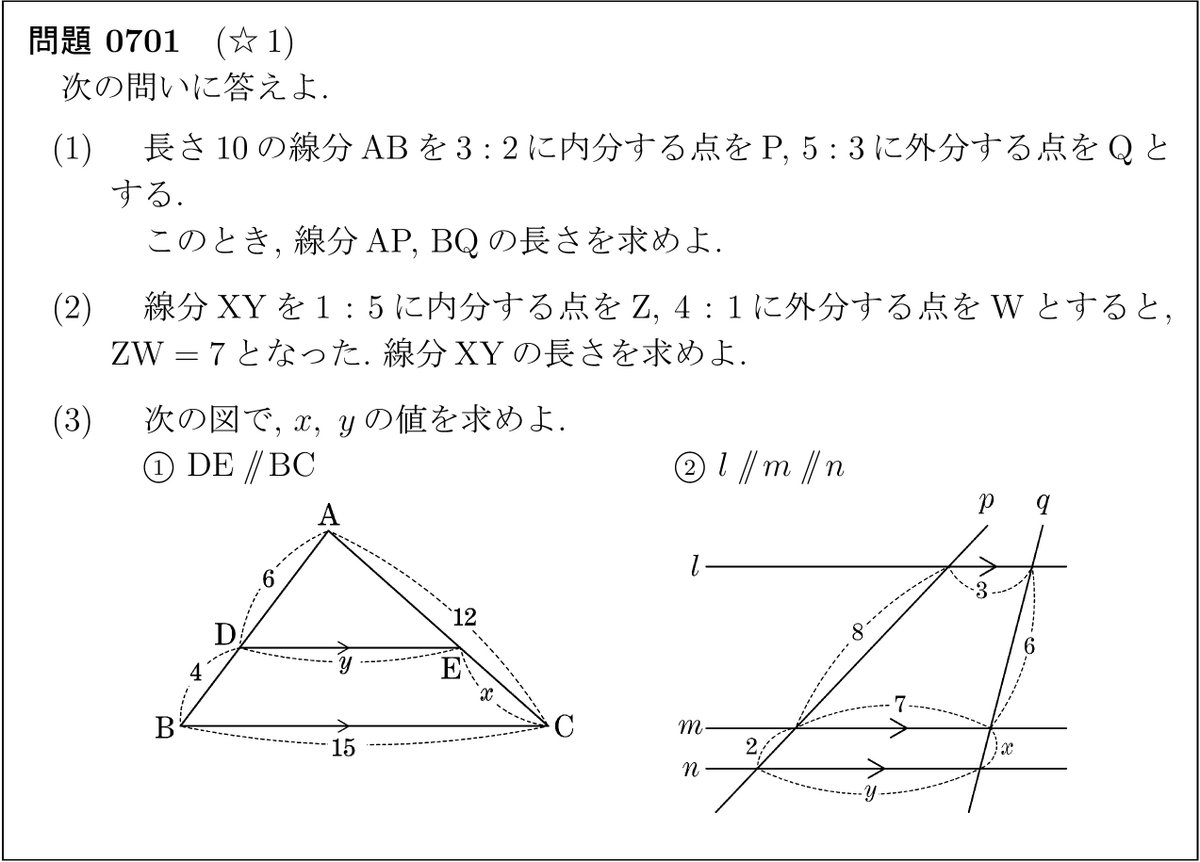



高校数学基本問題垂れ流し 07 図形の性質 1 三角形と比 線分の内分と外分 平行線と比 T Co Rvv5doaz7m
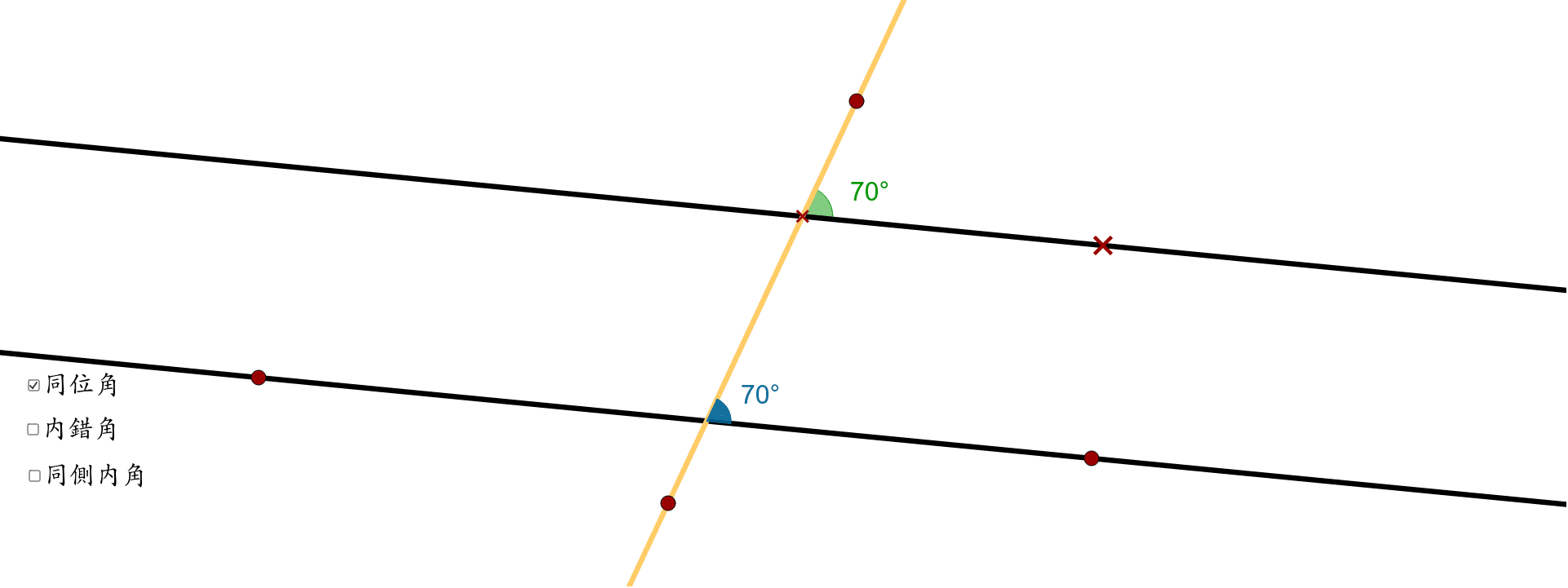



平行線的截線性質 Geogebra



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




平行線性質的3大技巧應用 考試你都會了麼 每日頭條




三角形の内角の和が180 になることの証明 数学fun




中学2年数学 図形の調べ方 平行線と角 練習問題4 あんのん塾
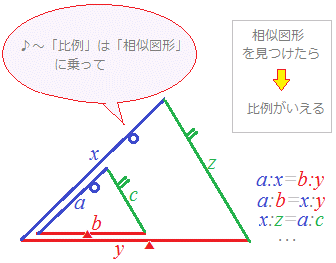



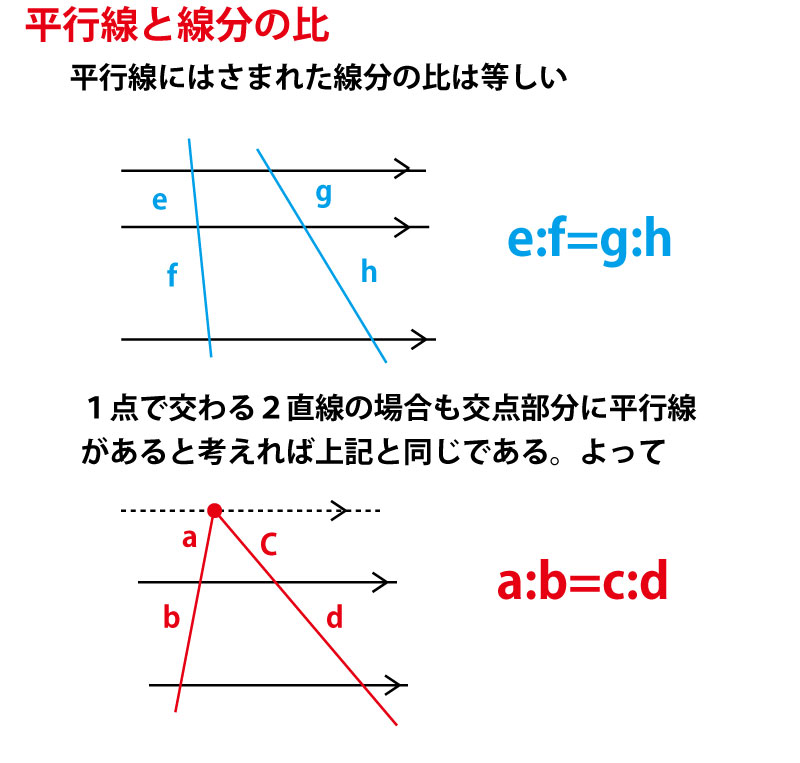
平行線と線分の比
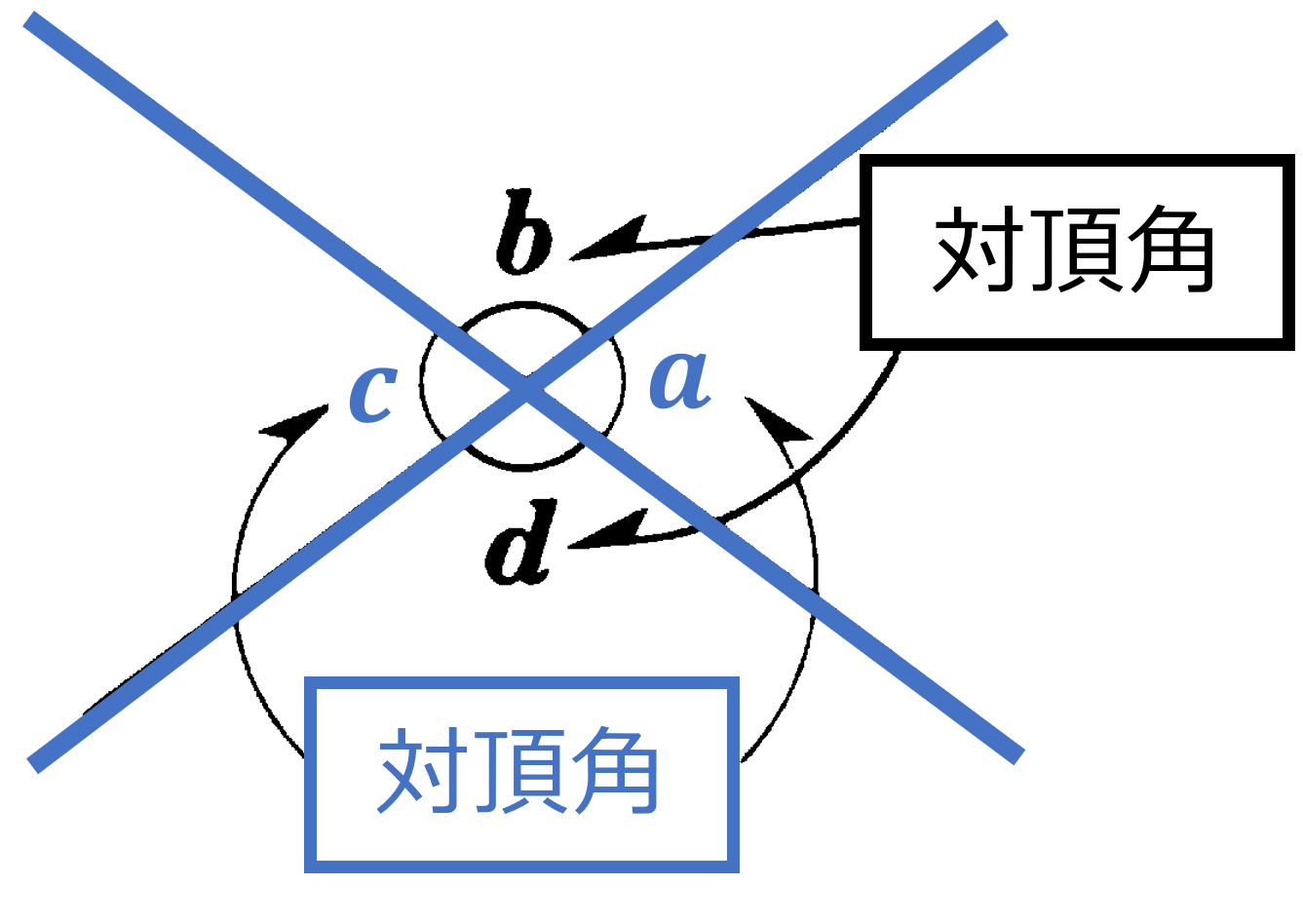



4章 図形の性質と合同 タカラゼミ




中学校2年 数学 アーカイブ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト
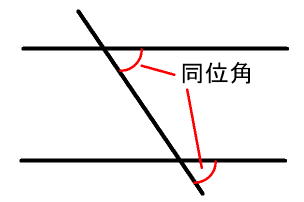



平行線と角



1




平行線の性質の背理法による証明の過程から一つ Okwave



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



指導手順 導入には図形の調べ方を学習するにあたって 図形を見た目だけで判断しないことが大事だということに気づかせるため 下記の2つのサイトから錯視をいくつかピックアップしてみせると盛り上がります スライド3 8まではスライドショーにしないで表示し 実際
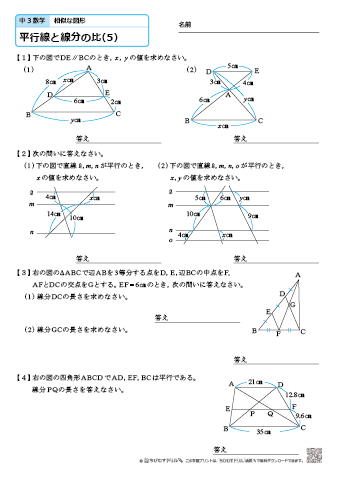



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
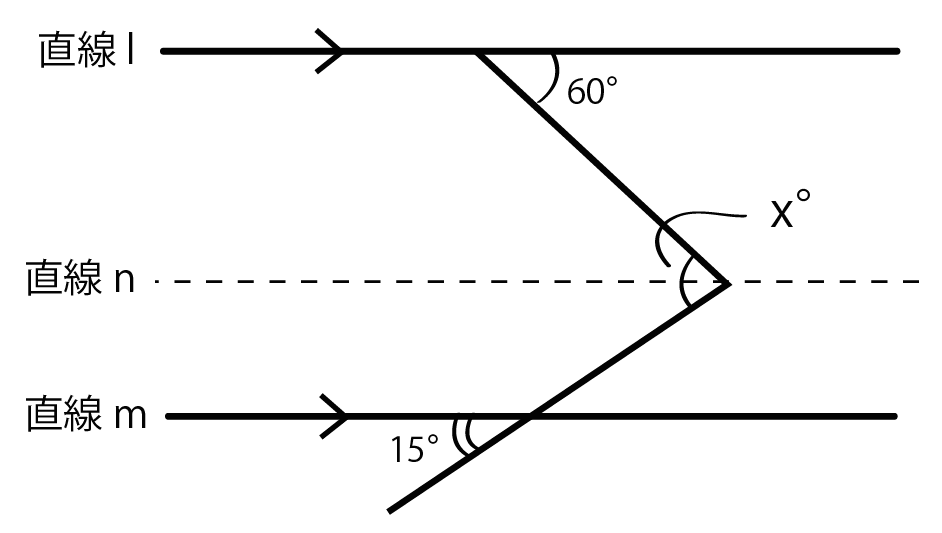



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく




平行線截角性質 Youtube




中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




高校数学a 平行線の性質のおさらい2 三角形 映像授業のtry It トライイット



Q Tbn And9gcs8yek Ytk4aevkupzlfiomyr1swah7y0fxr8n2 Yhcmpzyumt Usqp Cau




1研究中 9月 18
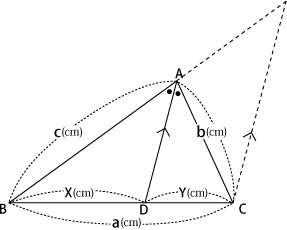



基礎学力アップシート 3年生 相似な三角形の線分の比を使おう




中2 図形の調べ方 最初 平行線の性質 Mathematics Quizizz
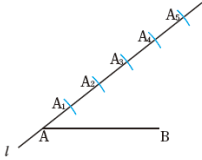



内分点と平行線の作図の仕方について 数学 苦手解決q A 進研ゼミ高校講座
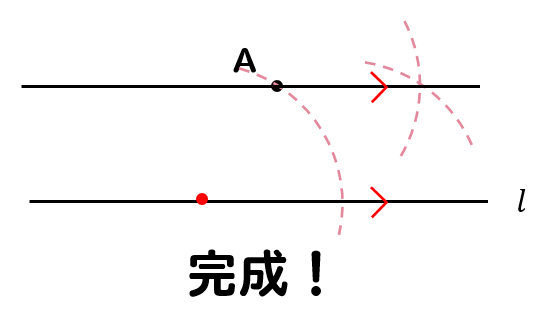



数学a作図 コンパスを使って平行線を作図する方法とは 数スタ
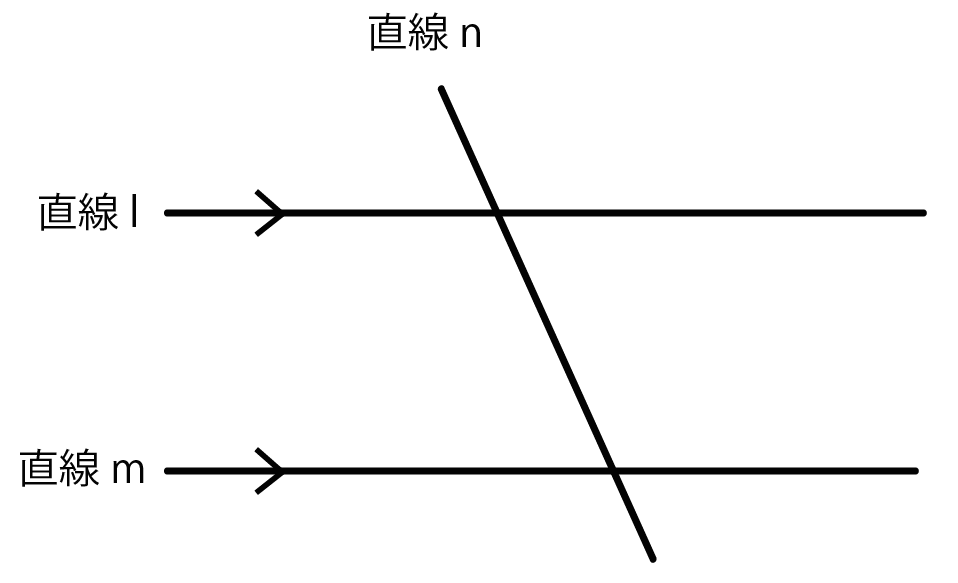



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく
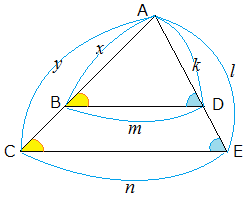



平行線と線分の比




中点連結定理 Wikipedia



平行線の同位角と錯角 中学から数学だいすき




錯角 同位角 対頂角の意味とは 平行線と角の性質をわかりやすく証明 応用問題アリ 中2数学 遊ぶ数学



Studydoctor平行線の錯角と同位角 中学2年数学 Studydoctor
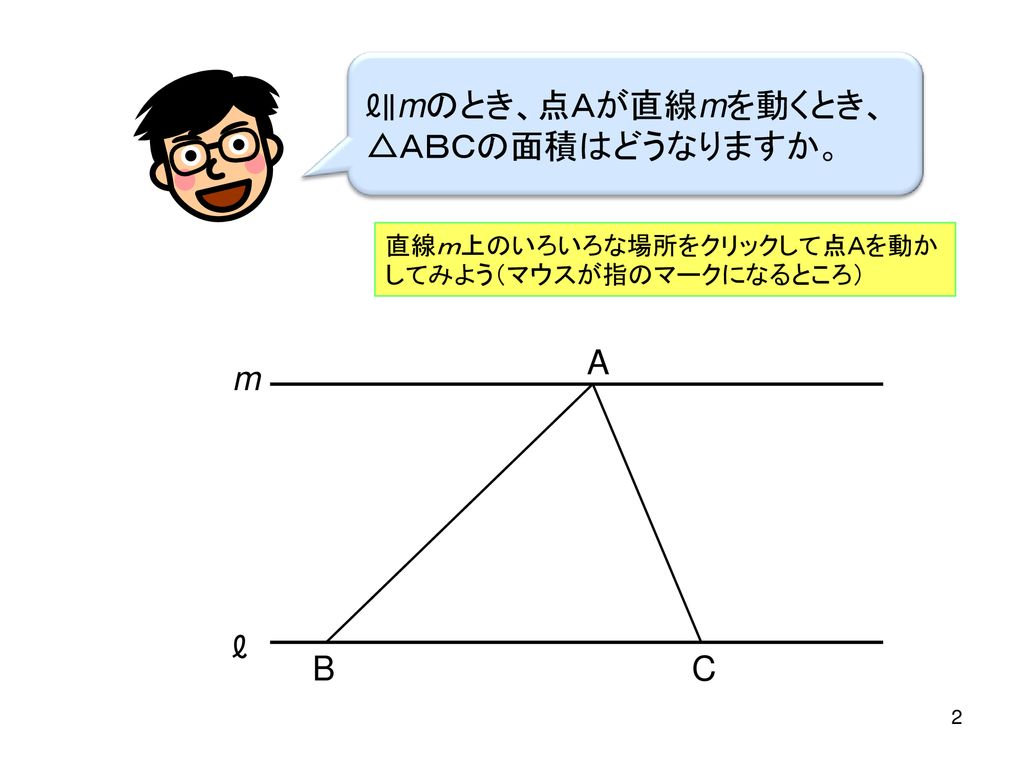



平行線の性質を使って 面積の等しい図形について考えてみよう Ppt Download
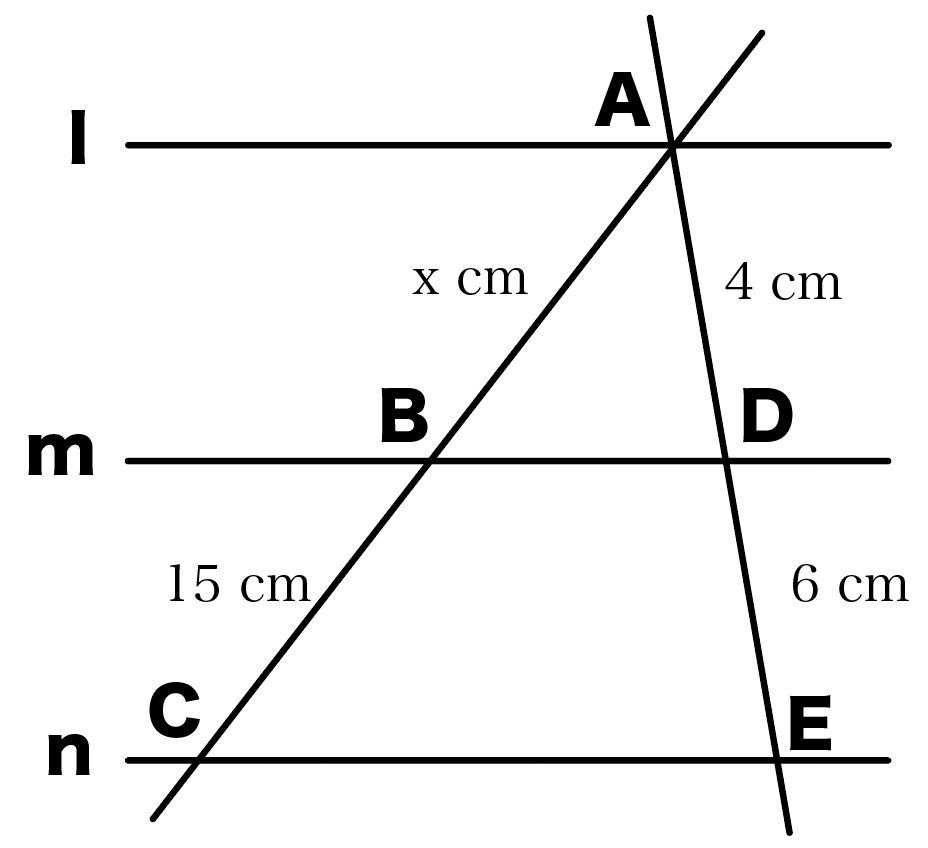



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Www Fuzoku Niigatajhs Jp Pdf Sugaku E6 95 B0 E5 Ad A6 E6 8e E6 A5 Ad E6 A1 Pdf



1




平行線公準 Wikipedia
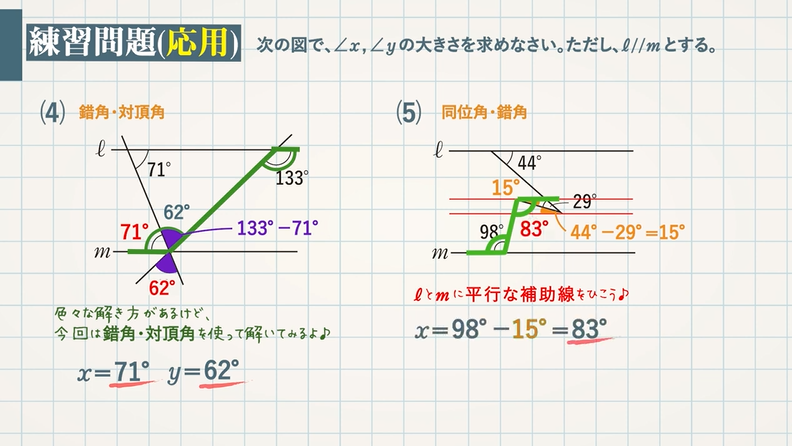



平行線と角 対頂角 錯角 同位角とは 教遊者
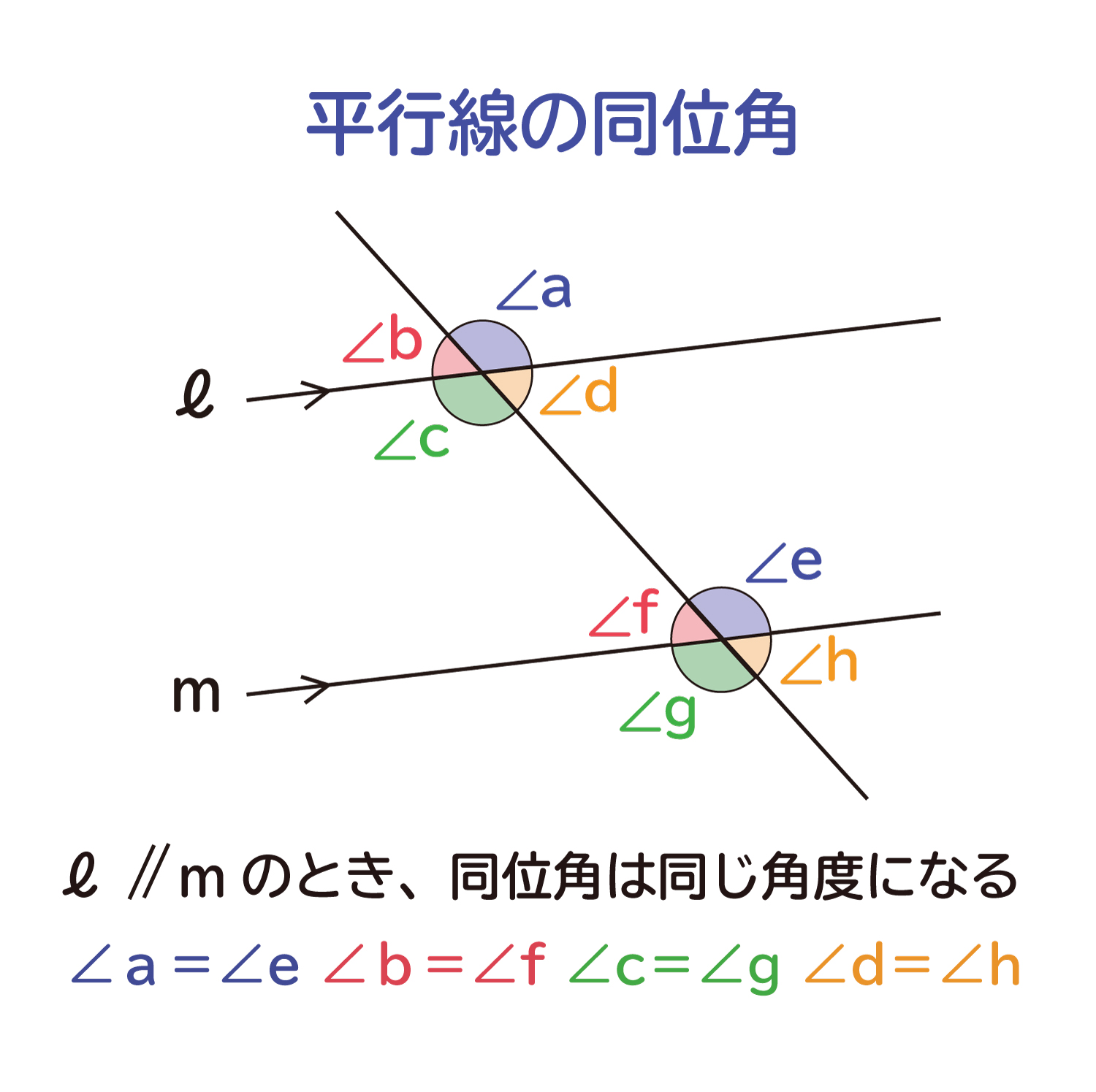



中学生の数学で出る平行線の同位角 どういかく と錯角 さっかく の性質 おかわりドリル
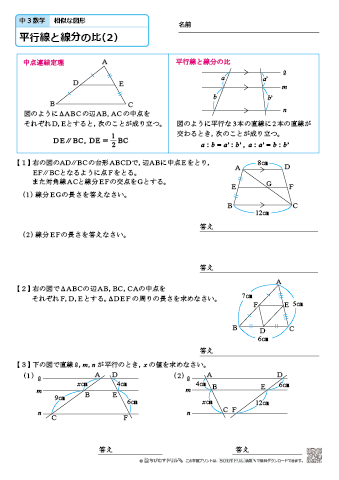



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
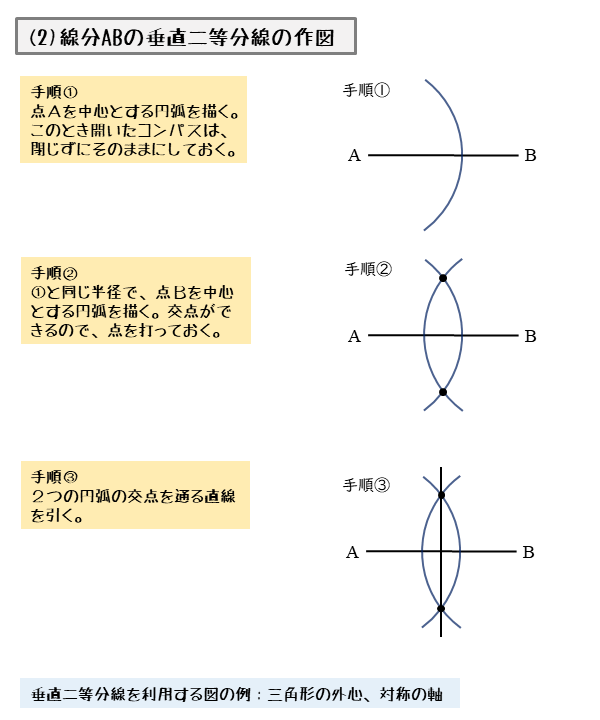



図形の性質 作図について 日々是鍛錬 ひびこれたんれん




折れ曲がってなければいいんでしょ 夢を叶える塾



Www Tsumugi Ne Jp Member St2 41 Pdf




一番上の問題の Clear




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2数学平行と合同についてです Clear
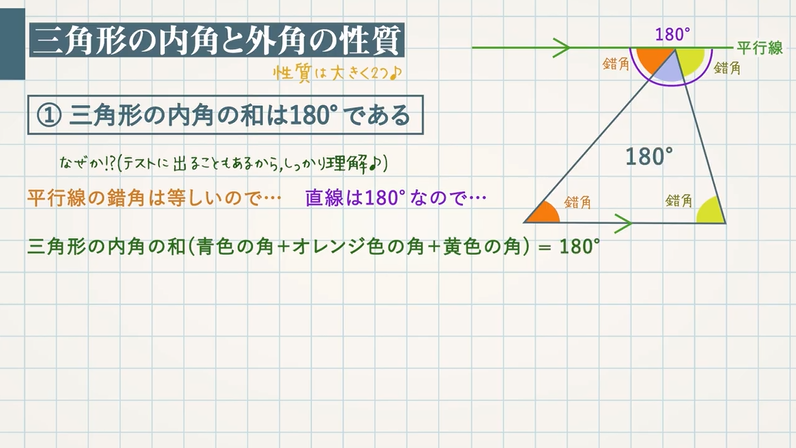



三角形の内角と外角の性質 教遊者



次の図において Xの値を求めよ という問題です 数学a平行線の性 Yahoo 知恵袋



Http Www Center Ibk Ed Jp Action Common Download Main Upload Id 5610




数学 中3 49 平行線と線分の比 基本編 Youtube




平行線と面積 等積変形 無料で使える中学学習プリント




中2数学 同位角 錯角 対頂角 図形の合同 ひっそりと物理や数学を解説する



エッシャーのように




スタディピア 図形




高校数学a 平行線の性質のおさらい2 三角形 映像授業のtry It トライイット
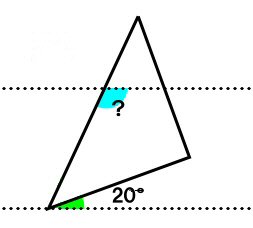



平行線と三角定規の作る角度2 3




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット



Studydoctor平行線と台形 中3数学 Studydoctor




中学数学 平行線と角 平行線の性質 Youtube




平行線の性質を使った証明 Youtube



中2平行線の性質の問題でxを求めなさいとあるのですがこの場合はどうやっ Yahoo 知恵袋




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




平行線と面積 で覚えておきたい2つのこと Qikeru 学びを楽しくわかりやすく


